3.1.6.26. HystereticSmooth Material (Smooth hysteretic material)
This command is used to construct the uniaxial HystereticSmooth material producing smooth hysteretic loops with hardening-softening behavior. It implements the “Exponential Material” formulated by Vaiana et al. [VaianaEtAl2018] based on an exponential formulation of the tangent stiffness.
- uniaxialMaterial HystereticSmooth $matTag $ka $kb $fbar $beta <-alpha>
Argument |
Type |
Description |
|---|---|---|
$matTag |
integer |
integer tag identifying material. |
$ka |
float |
Tangent stiffness of the initial “elastic” part of the loop. |
$kb |
float |
Tangent stiffness at zero displacement/strain. |
$fbar |
float |
Hysteresys force/stress at zero displacement/strain. |
$beta |
float |
Parameter governing hardening/softening behavior. |
-alpha |
string |
Optional flag: if activated the 3rd parameter is “alpha” instead of “fbar” (see below for the details). |
Note
Determination of constitutive parameters is quite intuitive and is reported below, although, their identification can be performed by the freeware available here.
The HystereticSmooth material provides the response sensitivity for reliability and parametric analysis. Possible calls for the parameters are ‘ka’, ‘kb’, ‘fbar’ and ‘beta’.
The equations describing HystereticSmooth behavior are described in [VaianaEtAl2018]. Only minor changes have been made in its implementation for OpenSees.
The model may reproduce either force-displacement or stress-strain relationships and behaves as a sort of smoothed bilinear model:
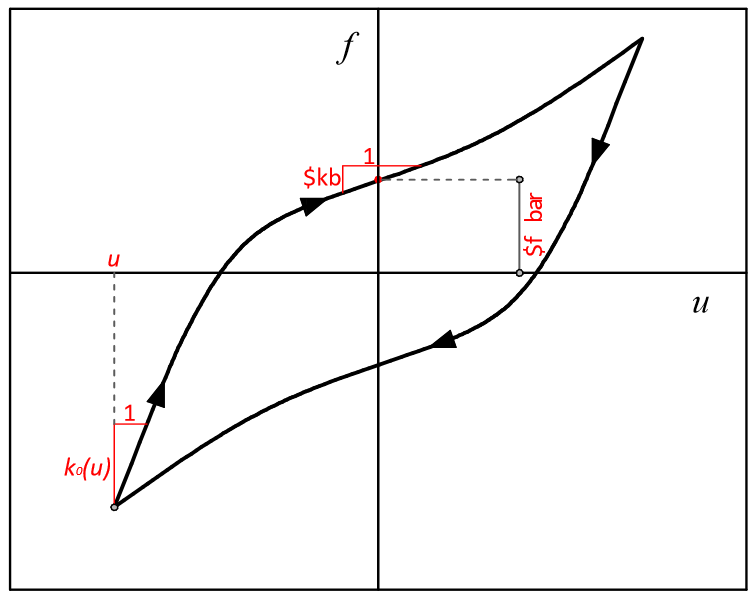
where $ka is the constant part of the initial tangent stiffness \(k_0(u) = k_a + \beta (-2+e^{\beta u}+e^{-\beta u})\) of each loop while $kb is the hysteresys force/strain at zero displacement. Yielding is ruled by a parameter \(\alpha\) determining the transition between the initial and final stiffness. This parameter is also related to the loop amplitude by means of:
\(\bar{f}=\frac{k_a-k_b}{2\alpha}\)
that is represented in figure. Because of the biunivocal relationship between \(\bar{f}\) and \(\alpha\), both can be used as input parameters. The default syntax uses \(\bar{f}\) although it is possible to provide \(\alpha\) by adding the flag “-alpha”.
Parameter $beta rules the hardening-softening behavior:
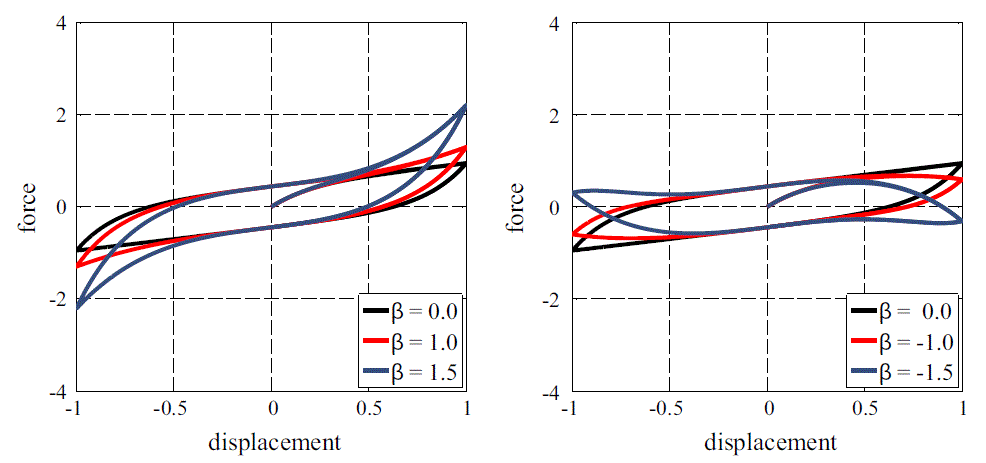
so that different loop shapes can be obtained:
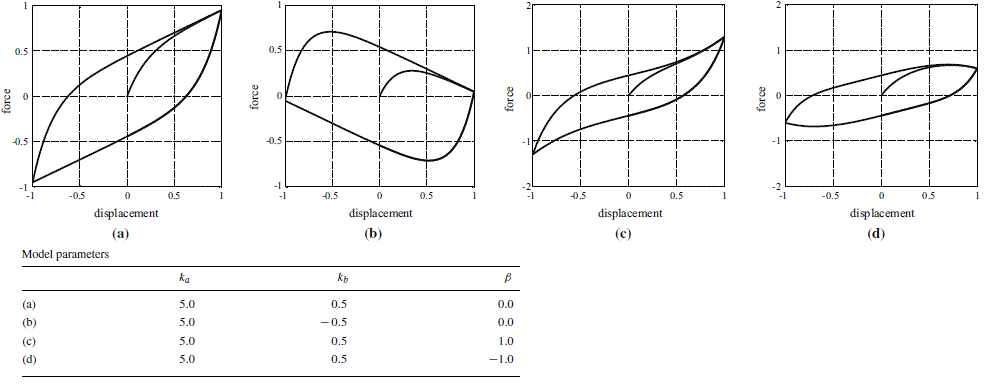
Example
The following constructs a HystereticSmooth material with tag 1, parameters corresponding to line (d) of the table above and $fbar=0.45.
Tcl Code
uniaxialMaterial HystereticSmooth 1 5.0 0.5 0.45 -1.0
Python Code
uniaxialMaterial('HystereticSmooth', 1, 5.0, 0.5, 0.45, -1.0)
Code Developed by: Salvatore Sessa, University of Naples Federico II, Italy
Vaiana, N., Sessa, S., Marmo, F. and Rosati, L. (2018). “A class of uniaxial phenomenological models for simulating hysteretic phenomena in rate-independent mechanical systems and materials.” Nonlinear Dynamics, 93(3): 1647-1669. DOI: https://doi.org/10.1007/s11071-018-4282-2